L'algoritmo Merge Sort è un algoritmo di ordinamento, sviluppato nel 1940 da John Von Neumann che consente di aggiornare una lista di elementi omogenei ricorrendo alla strategia divide et impera.
Rispetto agli algoritmi Bubble Sort ed Insertion Sort, che hanno prestazioni migliori con liste parzialmente ordinate, le prestazioni dell'algoritmo di Merge Sort non dipendono dal fatto che i dati di input siano ordinati.
Algoritmo
L'algoritmo Merge Sort è basato sulla strategia divide et impera; l'algoritmo per ordinare gli elementi lavora su due fasi:
- splitting: divide ricorsivamente la lista fino a quando la dimensione dei dati risulta inferiore rispetto ad una certa soglia
- merging: elabora i dati fino a restituire il risultato finale
Se ad esempio volessimo applicare le due fasi alla lista [56, 52, 25, 69, 14, 3], l'elaborazione prevede i seguenti passaggi di ordinamento.
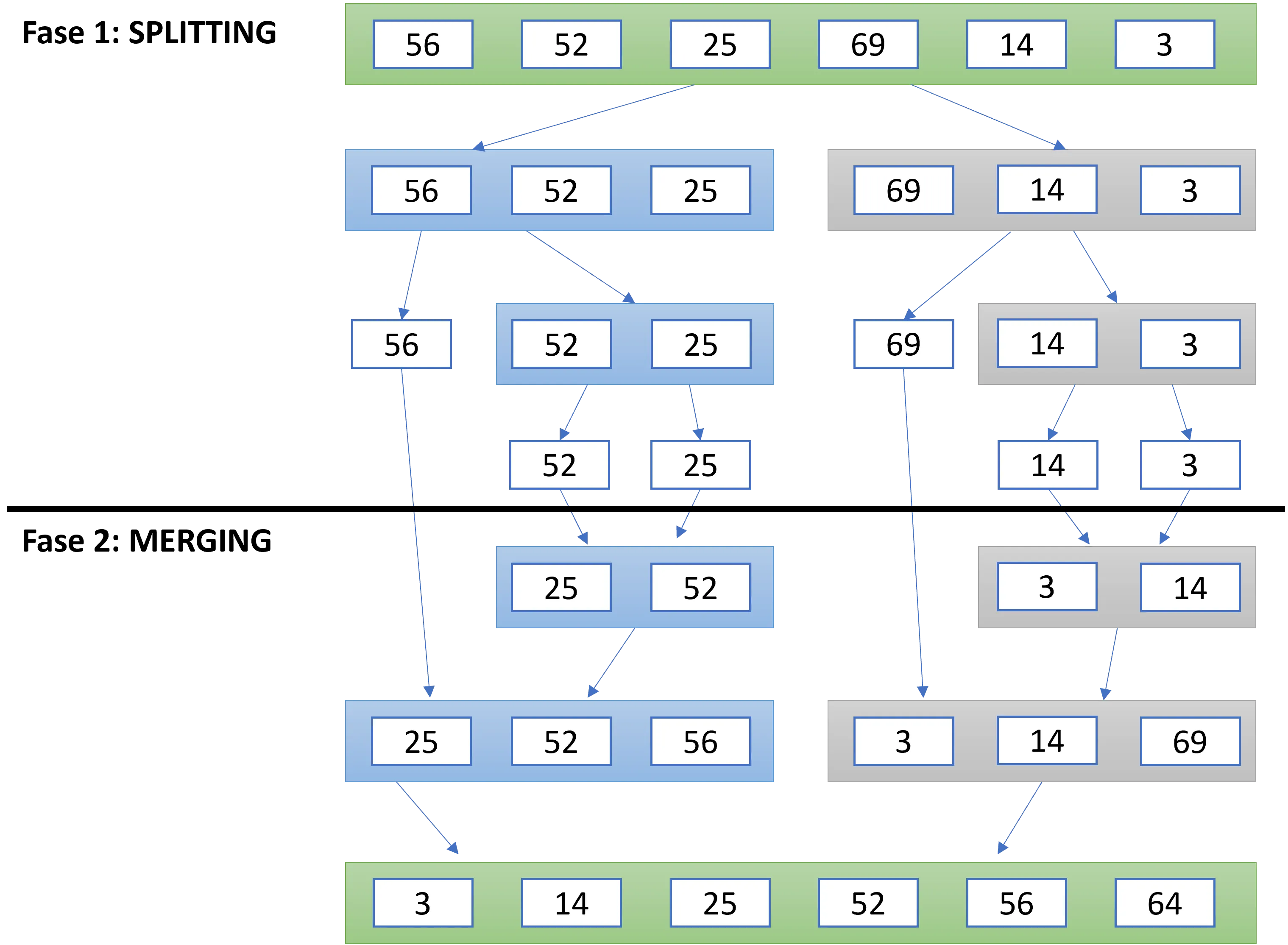
L'algoritmo esegue logicamente questi tre passaggi:
- Divide la lista di elementi in parti uguali
- Ricorsivamente divide le liste finchè tutte le sottoliste abbiano lunghezza
pari ad
1 - Unisce le sottoliste ordinate in una lista ordinata e le restituisce
Implementazione
L'implementazione in Python dell'algoritmo Merge Sort è la seguente:
def merge_sort(elements):
if len(elements) > 1:
# fase 1: splitting
mid = len(elements) // 2
left = elements[:mid]
right = elements[mid:]
merge_sort(left)
merge_sort(right)
# fase 2: merging
a = b = c = 0
while a < len(left) and b < len(right):
if left[a] < right[b]:
elements[c] = left[a]
a += 1
else:
elements[c] = right[b]
b += 1
c += 1
while a < len(left):
elements[c] = left[a]
a += 1
c += 1
while b < len(right):
elements[c] = right[b]
b += 1
c += 1
return elements
L'implementazione prevede delle chiamate ricorsive alla funzione finchè la lunghezza della lista degli elementi non risulta pari ad 1. A quel punto si avvia la fase di merging andando ad ordinare le sottoliste che man mano si vanno a formare.
Prestazioni
L'algoritmo Merge Sort ha una complessità O(n log n) nel suo caso medio e peggiore.
Se andiamo a vedere come si comporta l'algoritmo notiamo che:
- ogni chiamata alla funzione
merge_sortha complessità O(n) - ogni funzione
merge_sortrichiama se stessa due volte con un numero di elementi di input dimezzati
Conclusioni
L'articolo mostra l'algoritmo di ordinamento Merge Sort che rappresenta un miglioramento rispetto agli algoritmi Bubble Sort ed Insertion Sort.
L'algoritmo rappresenta una soluzione di ordinamento anche per elenchi di dimensioni elevate data la sua complessità O(n log n) nel caso peggiore.
L'implementazione dell'algoritmo è leggermente più complessa rispetto ad altri algoritmi di ordinamento.




