In questo articolo, imparerai le nozioni alla base dell'algoritmo e vedrai una sua implementazione nel linguaggio Python.
L'algoritmo Shell Sort è un algoritmo di ordinamento che generalizza l'algoritmo Insertion Sort. L'algoritmo prevede l'ordinamento di coppie di elementi distanziati di un certo numero di elementi, iterando tale approccio (a ritroso) fino al completo ordinamento dell'elenco dati iniziale.
L'intervallo di elementi utilizzato, attraverso il quale si procede
all'ordinamento, dipende dalla sequenza usata. La sequenza standard utilizzata
dall'algoritmo prevede come intervalli: N/2, N/4, N/8, ..., 1.
dove N rappresenta il numero di elementi da ordinare.
Da notare che le prestazioni dell'algoritmo dipendono dal tipo di sequenza utilizzata per una dato input di dati.
Strategia di ordinamento
Si supponga di dover ordinare il seguente elenco di elementi:

Ipotiziammo l'utilizzo della sequenza standard, e quindi divideremo il nostro
elenco in intervalli: N/2, N/4, ..., 1.
Primo ciclo N/2
Nel primo ciclo la sequenza ha dimensione N=8, l'algoritmo prende come
intervallo N/2 = 4 e quindi gli elementi sono comparati a coppie di distanza
pari a 4 eseguendo le seguenti iterazioni.
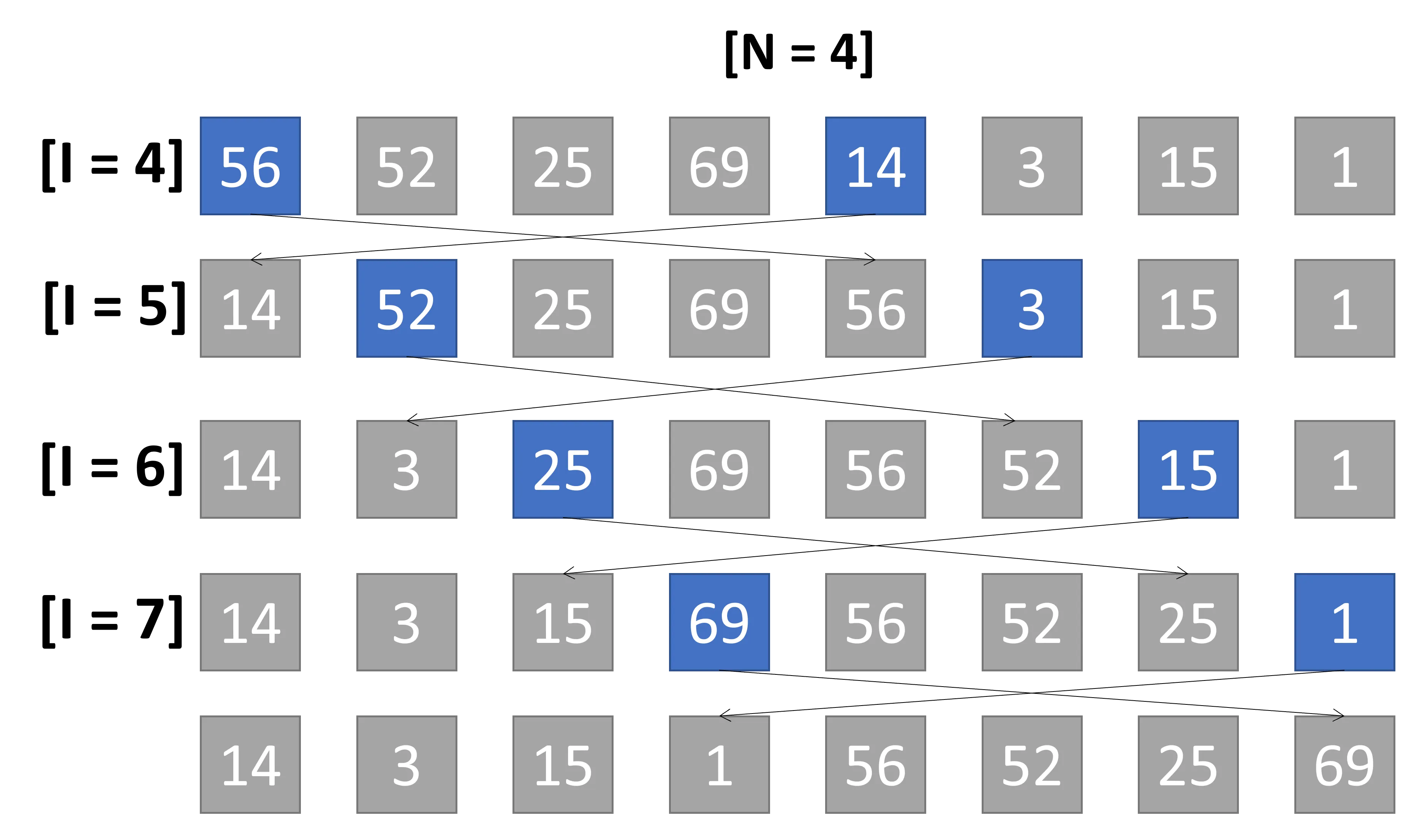
Ogni comparazione prevede lo spostamento degli elementi; si ha una spostamento, se l'elemento con indice inferiore risulta essere maggiore dell'elemento con indice maggiore.
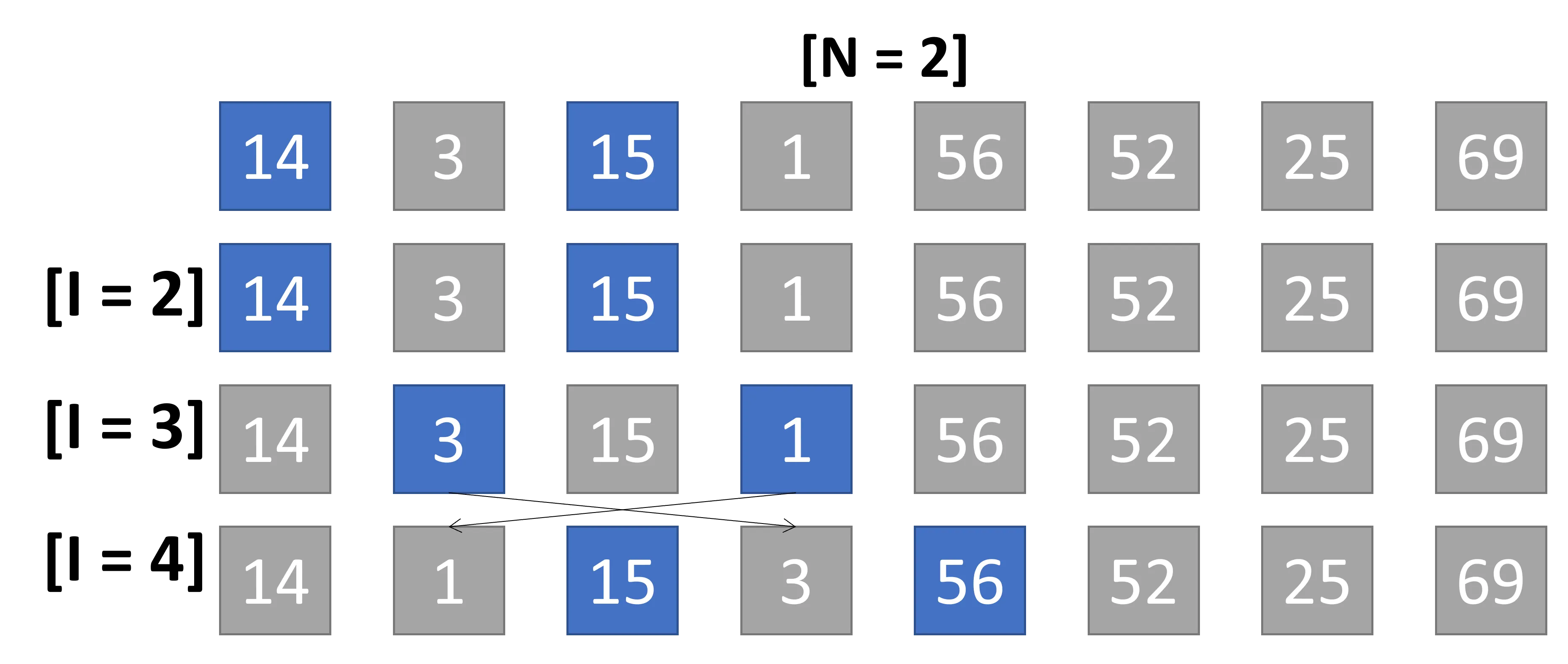
Secondo ciclo N/4
Il secondo ciclo prevede un intervallo pari a N/4 = 8/4 = 2. Le iterazioni in
questo intervallo sono:
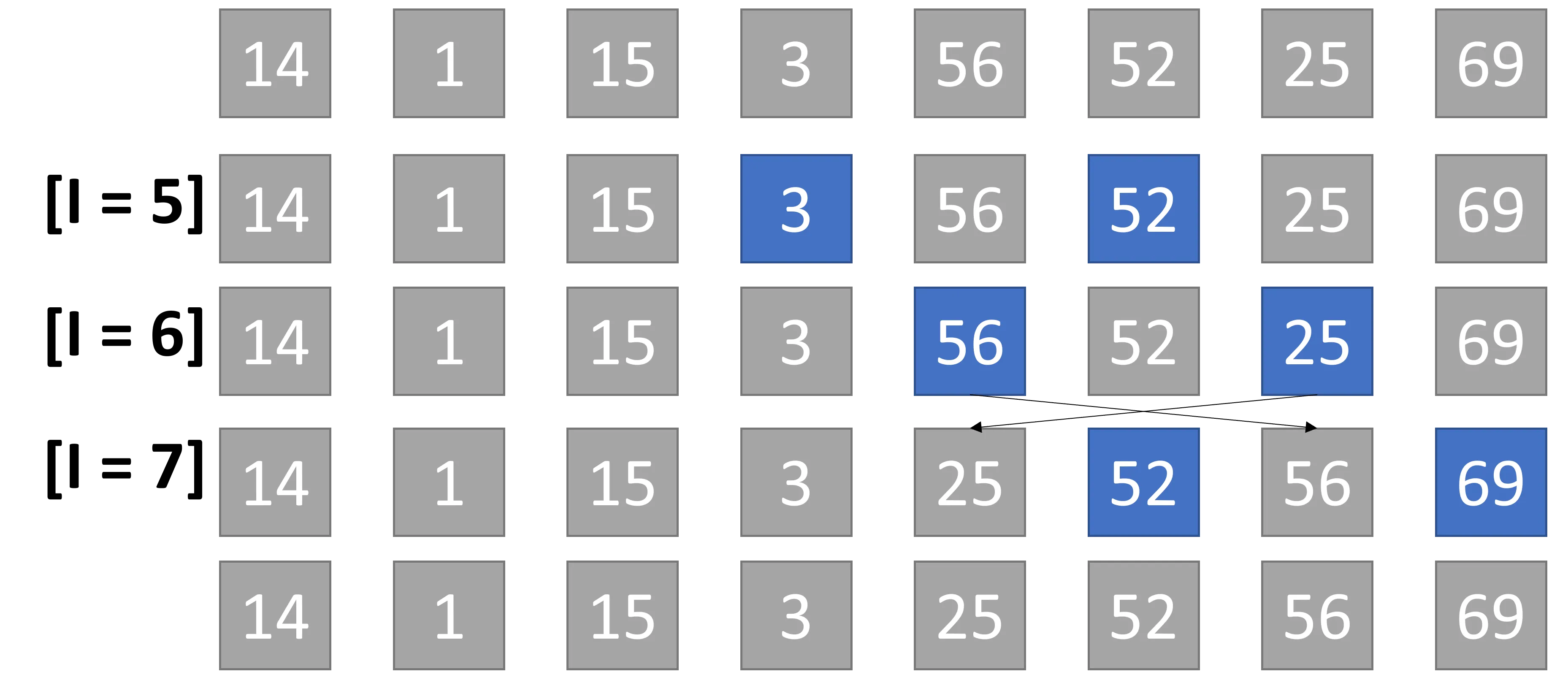
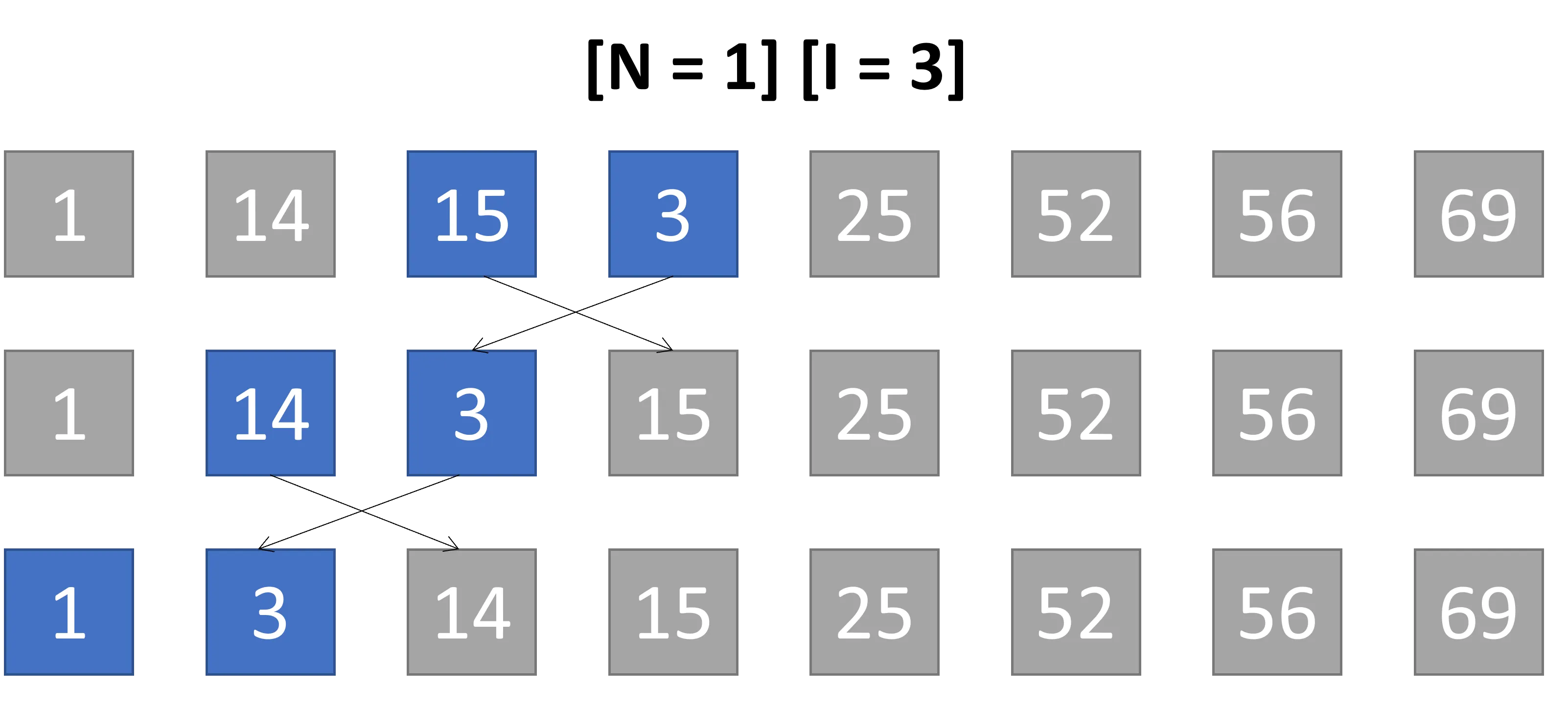
Terzo ciclo N/8
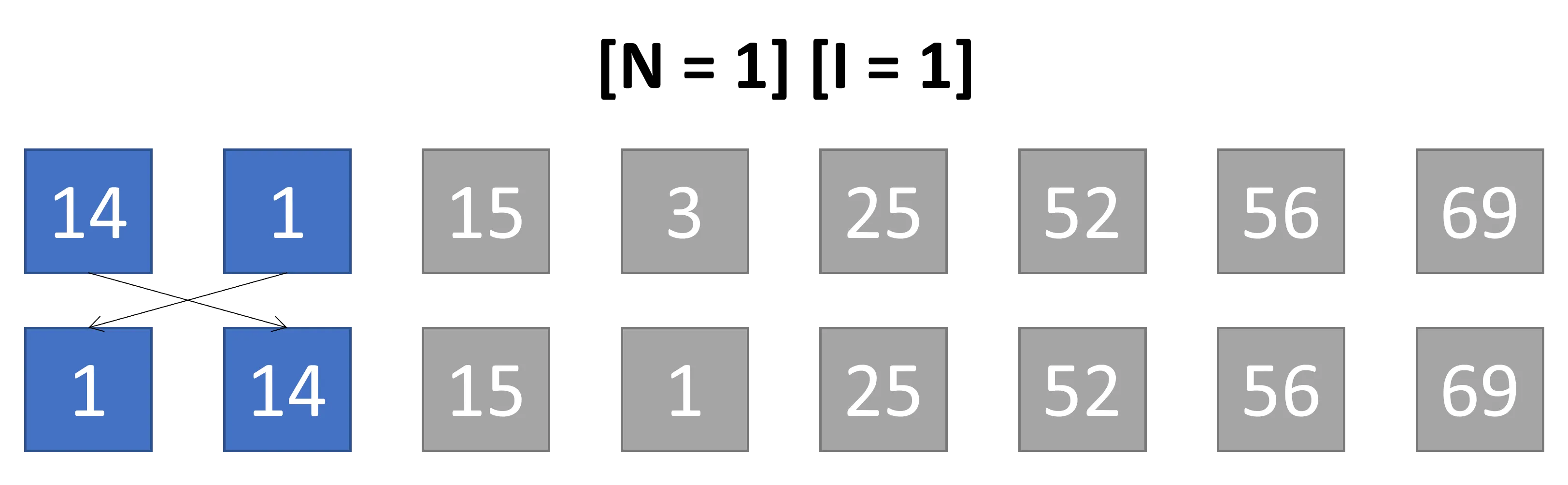
Nella successiva iterazione N/8 = 8/8 = 1 sono comparati gli elementi vicini
per ordinare tutti gli elementi:
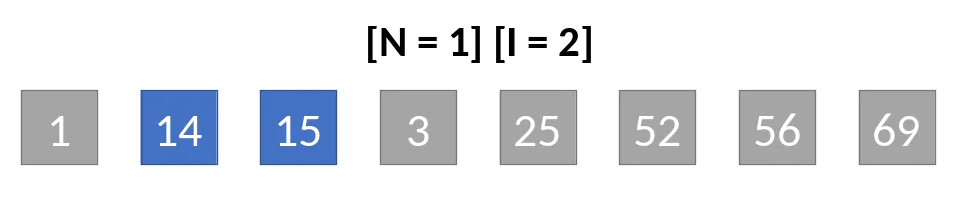




Implementazione (in Python)
Implementiamo in Python l'algoritmo Shell Sort come segue:
def shell_sort(elements):
interval = len(elements) // 2
size = len(elements)
while interval > 0:
for i in range(interval, size):
temp = elements[i]
j = i
while j >= interval and elements[j - interval] > temp:
elements[j] = elements[j - interval]
j -= interval
elements[j] = temp
interval //= 2
return elements
Prestazioni
L'algoritmo Shell Sort offre le seguenti prestazioni:
| Caso | Complessità |
|---|---|
| Migliore | O(n log n) |
| Medio | O(n log n) |
| Peggiore | O(n²) |
Il caso migliore si ha quando l'array è ordinato, nel qual caso il numero di comparazioni per ogni incremento è pari alla dimensione dell'elenco.
Conclusioni
L'algoritmo di Shell Sort può essere utilizzato con un numero di elementi considerevole ma che non superi le 5000 unità. Funziona bene se i dati sono parzialmente ordinati.
L'algoritmo non è da utilizzare con i Big Data visto la sua cattiva predisposizione ad ordinare un numero elevato di elementi.




